Met de functie FACULTEIT kun je de faculteit van een getal berekenen.
De faculteit van een getal is het resultaat van alle positieve gehele getallen tot en met dat getal met elkaar vermenigvuldigd.
In de wiskunde wordt dit vaak weergegeven met een uitroepteken, bijvoorbeeld 5!.
Dit komt neer op 1 * 2 * 3 * 4 * 5 = 120
Wanneer gebruik je deze functie?
In de praktijk gebruik je de functie vooral bij kansberekeningen, zoals het bepalen van het aantal mogelijke combinaties of volgordes.
Schrijfwijze formule
=FACULTEIT(getal)
Argumenten
Het enige argument is getal. Hier voer je het getal (of de celverwijzing) in waarvan je de faculteit wilt berekenen.
- Als het getal geen geheel getal is, wordt het automatisch naar beneden afgerond.
- Negatieve getallen resulteren in een foutmelding.
Hoe deze functie werkt
=FACULTEIT(4)resulteert in 24 ( 1 * 2 * 3 * 4 = 24)- =FACULTEIT(2,7) resulteert in 2 ( 1 * 2 = 2)
=FACULTEIT(0)resulteert in 1 (1 (0! is in de wiskunde gedefinieerd als 1)

Voorbeeld 1: Permutaties van cijfers
Nu je weet hoe de functie werkt, gaan we kijken naar een wat meer praktisch voorbeeld.
Stel, je wilt weten op hoeveel manieren je 5 cijfers kunt kiezen uit een reeks van 10 cijfers (0 t/m 9), waarbij elk cijfer maar één keer mag worden gebruikt en de volgorde telt mee.
Het aantal mogelijkheden bereken je met de volgende formule: =FACULTEIT(10)/FACULTEIT(10-5)
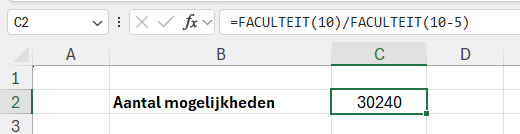
Dit werkt als volgt:
FACULTEIT(10)= 1 × 2 × … × 10 = totaal aantal volgordes van 10 cijfersFACULTEIT(10-5)= FACULTEIT(5) = aantal manieren waarop de resterende 5 cijfers gerangschikt kunnen worden- Door te delen krijg je het aantal mogelijke volgordes van 5 cijfers uit 10, dus 30.240 mogelijkheden.
Voorbeeld 2: kansberekening
Stel je wilt berekenen hoeveel verschillende volgordes mogelijk zijn als je drie worpen met een dobbelsteen doet. Je mag hierbij geen cijfer herhalen.
De formule hiervoor is =FACULTEIT(6)/FACULTEIT(6-3) wat resulteert in 120 mogelijkheden.
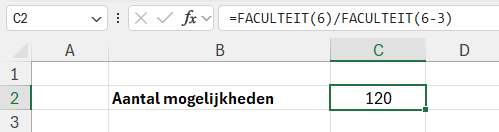
Dit werkt als volgt:
FACULTEIT(6)berekent 1 * 2 * 3 * 4 * 5 * 6 = 720- 6-3 = 3, dus
FACULTEIT(6-3)berekent 1 * 2 * 3 = 6 - 720 gedeeld door 6 = 120
Een dobbelsteen bestaat uit 6 items en je wilt er in dit voorbeeld 3 kiezen. Met deze formule heb je dus berekent dat er er 120 verschillende mogelijkheden zijn om die 3 items te rangschikken.
Met andere woorden, de formule heeft het aantal mogelijke reeksen berekent van 3 uit 6 items.
Weet je nooit welke formule je nodig hebt
in Excel?
In mijn cursus leer je stap voor stap hoe je formules opbouwt en combineert. Alles wordt op een laagdrempelige en gestructureerde manier uitgelegd, met praktische voorbeelden en oefeningen.
Je ontdekt hoe formules echt werken, zodat je precies weet wat je moet invullen. Na de cursus kun je met vertrouwen zelf formules maken, van eenvoudige berekeningen tot meer complexe toepassingen.



